Small Tension and Compression Load Cell 1kg/3kg/5kg/20kg/200kg
This time we will introduce a small load cell. It is a tension and compression load cell for force measurement, such as automobile braking force detection.
Load cell specification:
Load cell dimension:
The elastic element of tension and compression load cell measure the bending stress of the circular plate.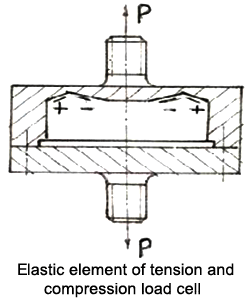 
Structural and mechanical characteristics of load cell elastic elements:
Maximum stress:
Maximum deflection:
Where, K and K1 are the stress and deflection computing coefficient. According to the ratio of the circular-plate elastic elements' supporting marginal radius, b, to the central loading convex platform radius, a, the convex platform circular-plate stress and deflection computing coefficient, K and K1, can be obtained.
Load cell specification:
|
Model |
ATO-S-LCC-DYMH-103 |
|
Weight |
0.1kg |
|
Capacity |
1kg, 2kg, 3kg, 5kg, 10kg, 20kg, 30kg, 50kg, 100kg, 150kg, 200kg |
|
Accuracy |
0.03%F.S (linearity + hysteresis + repeatability) |
|
Sensitivity |
1.0~1.5mV/V |
|
Creep |
±0.05%F.S/30min |
|
Zero output |
±1%F.S |
|
Temperature effect on zero |
±0.05%F.S/10℃ |
|
Temperature effect on output |
±0.05%F.S/10℃ |
|
Operating temperature |
-30℃~+70℃ |
|
Input impedance |
400±10Ω |
|
Output impedance |
350±10Ω |
|
Insulation resistance |
≥5000MΩ |
|
Safety overload |
150%F.S |
|
Overload limit |
200%F.S |
|
Bridge voltage |
DC 10-15V, suggest DC 10V |
|
Material |
Stainless steel |
|
Protection class |
IP67 |
|
Cable length |
2m |
|
Wiring |
EXC+: Red, EXC-: Black, SIG+: Green, SIG-: White |
|
Capacity |
M |
|
5kg, 10kg, 15kg, 20kg, 30kg, 50kg |
M5 |
|
60kg, 100kg |
M6 |
|
200kg |
M8 |
Structural and mechanical characteristics of load cell elastic elements: - Simple and compact structure, small volume, low height, and light.
- Circular appearance, easy to ensure high processing precision of dimensions, form and position.
- Large transverse stiffness and strong resistance against eccentricity and lateral load.
- An integrated circular and symmetric circular plate. Consistent in different directions of thermal expansion. Low temperature coefficient.
- Simple theoretical computing. The maximum deflection, W, is far smaller than the circular-plate thickness, h, under the effect of the external load, so the thin-plate small deflection bending theory is applicable. Capable of being simplified into the surrounding fixed support.
Maximum stress:
Maximum deflection:
Where, K and K1 are the stress and deflection computing coefficient. According to the ratio of the circular-plate elastic elements' supporting marginal radius, b, to the central loading convex platform radius, a, the convex platform circular-plate stress and deflection computing coefficient, K and K1, can be obtained.